When steel is curved, it is important to keep the stress-strain curve ratio for mild steel in mind. Below is a stress-strain graph that reviews the properties of steel in detail.
If tensile force is applied to a steel bar, it will have some elongation. If the force is small enough, the ratio of the stress and strain will remain proportional. This can be seen in the graph as a straight line between zero and point A – also called the limit of proportionality. If the force is greater, the material will experience elastic deformation, but the ratio of stress and strain will not be proportional. This is between points A and B, known as the elastic limit.
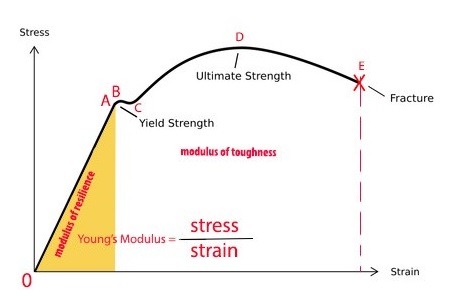
Beyond the elastic limit, the mild steel will experience plastic deformation. This starts the yield point – or the rolling point – which is point B, or the upper yield point. As seen in the graph, from this point on the correlation between the stress and strain is no longer on a straight trajectory. It curves from point C (lower yield point), to D (maximum ultimate stress), ending at E (fracture stress).
Now, we’ll look at each individual measure on the graph above and explain how each is derived.
- Stress: If an applied force causes a change in the dimension of the material, then the material is in the state of stress. If we divide the applied force (F) by the cross-sectional area (A), we get the stress.
The symbol of stress is σ (Greek letter sigma). For tensile (+) and compressive (-) forces. The standard international unit of stress is the pascal (Pa), where 1 Pa = 1 N/m2. The formula to derive the stress number is σ = F/A.
For tensile and compressive forces, the area taken is perpendicular to the applied force. For sheer force, the area is taken parallel to the applied force. The symbol for shear stress is tau (τ).
- Strain: Strain is the change in the dimension (L-L0) with respect to the original. It is denoted by the symbol epsilon (ε). The formula is ε = (L-L0) / L0. For a shear force, strain is expressed by γ (gamma)
- Elasticity: Elasticity is the property of the material which enables the material to return to its original form after the external force is removed.
- Plasticity: This is a property that allows the material to remain deformed without fracture even after the force is removed.
The definitions below are important for understanding the Stress-Strain interactions as seen in the graph.
- Hooke’s Law: Within the proportional limit (straight line between zero and A), strain is proportionate to stress.
- Young’s modulus of elasticity: Within the proportional limit, stress = E × strain. E is a proportionality constant known as the modulus of elasticity or Young’s modulus of elasticity. Young’s modulusis a measure of the ability of a material to withstand changes in length when under lengthwise tension or compression. E has the same unit as the unit of stress because the strain is dimensionless. The formula is E = σ / ε Pa.
- Modulus of Resilience: The area under the curve which is marked by the yellow area. It is the energy absorbed per volume unit up to the elastic limit. The formula for the modulus of resilience is 1/2 x σ x ε = 0.5 x (FL/AE).
- Modulus of toughness: This is the area of the whole curve (point zero to E). Energy absorbed at unit volume up to breaking point.
Chicago Metal Rolled Products sets the industry standard for adherence to the stress strain curve for mild steel and other materials. Contact one of our estimators today.







