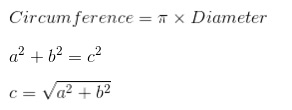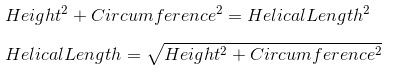Here’s a quick lesson that will take you back to your days of high school algebra, and may help in estimating material needed for helically rolled projects.
The curved arc length of a helical item, used for a number of applications such as handrails, stair stringers, and helical strakes can be quickly calculated using some simple formulas.
We need to know the circumference equation and the Pythagorean Theorem for calculating the hypotenuse of a triangle:
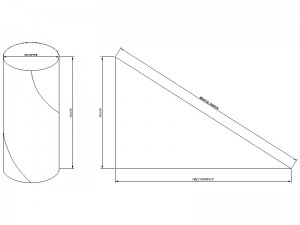
In the example image at the bottom, we have a 360 degree helical curve wrapping around a cylinder. If we know the height and diameter of the cylinder, we can calculate the helical length. If you were to take the cylinder and roll it out, the helical length would form the hypotenuse of a triangle made by the height of the cylinder, and it’s circumference.
So, in this example, if the Height of the cylinder = 10 feet (120 inches), and the Diameter = 5 feet (60 inches), then the Circumference (3.14 x 5) = 15.7 feet, and the Helical Length = 18.6 feet
You can use this method for calculating lengths that aren’t a complete 360 degrees either.
Just substitute the plan view arc length of the helical curve for the circumference arc length, and the overall rise for the height of the cylinder.